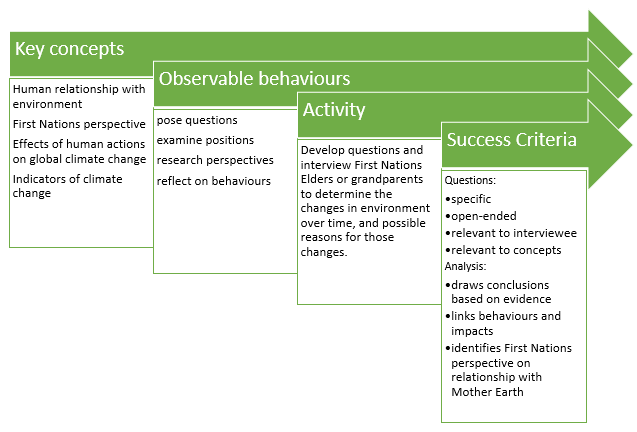
How often have we been in a conversation with a colleague about trying to meet the needs of all of our students, and we hear the dreaded phrase “well, just differentiate”… this blanket statement can bring about visions of creating 18 different lesson plans for our 18 students. This is not sustainable, so what is differentiation REALLY? How do we meet the needs of diverse learners and keep our sanity?
Workshops focussing on differentiation are, ironically, often not differentiated. It is important that all professional learning, including those experiences based on the topic of differentiation, attempt to have teachers experience differentiated learning as well as reinforce the foundations of how and why we differentiate content, process, product and environment for students.
Planning for Differentiation
It is important to understand not only specific strategies but to also know why we might differentiate. What information do we need as teachers in order to plan appropriately for our individual students as well as our whole class experiences? We need to know a combination of Learning Styles, Multiple Intelligences, content readiness, and student interests in order to Plan for Differentiation.
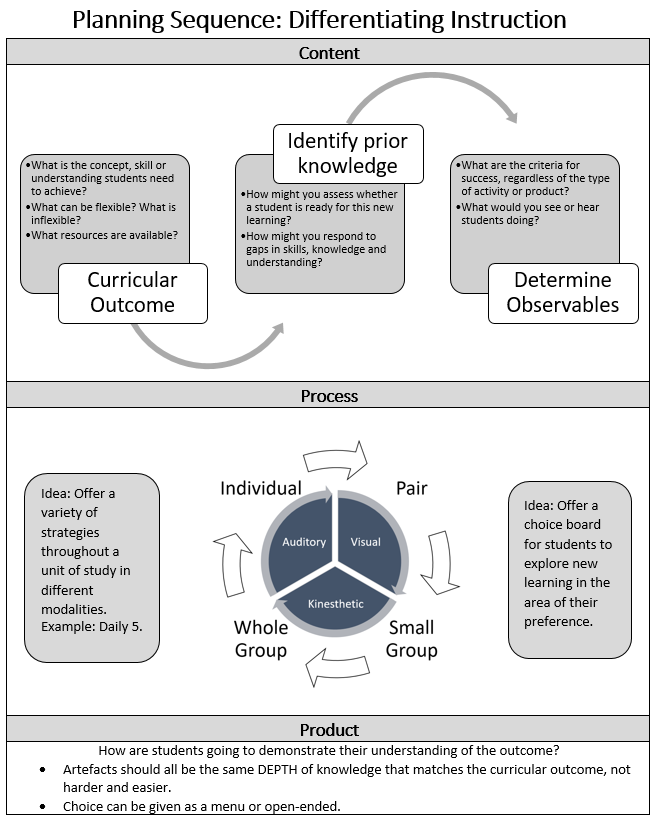
This information can be compiled into a Learner Profile Card or a Whole-Class Preferences Summary Chart to allow both students and teachers to know what and how learners might learn best.
Something that is often an ‘aha’ for adults is to consider whether they are “Think to Talk or Talk to Think” learners. If someone is a think-to-talker and is forced to jump into group work without first having the chance to get their thoughts in order, they may have a feeling of being unsafe expressing their ideas. If a talk-to-thinker is forced to read quietly before they are allowed to talk, they may find that their minds wander and are unable to focus. This same sense of safety is true for student learners as well.
One of the foundational researchers in the area of differentiation is Carol Tomlinson, who describes differentiation as
- Being curious about our students,
- Having relationships between teachers and students; and
- Providing a variety of learning experiences to learners
Differentiating Content
Why:
Differentiating content allows you to address gaps in understanding to build readiness. We know in literacy that activating prior knowledge is essential for students to make connections to new learning. This is true in other subjects as well. Assessing prior knowledge allows gaps to be addressed before new concepts are introduced. Differentiating content allows students to ACCESS information and learning.
What:
Your curriculum drives the knowledge, concepts, skills, and understandings a student needs to know and use. While the curricular outcome cannot change for individual students, the delivery format for content such as video, readings, audio, reading level can be differentiated. Content can also be chunked, shared through visual graphic organizers, or addressed through jigsaws to reduce the volume of information each individual needs to interact with. Themes can be based on personal interest to increase interest and understanding if a specific topic is not required by the curriculum.
How:
- Use pre-assessment to determine where students need to begin, then match students with appropriate activities. Pre-assessments may include:
- Student/teacher discussion,
- Begin a KWL chart – what we know/want to know/learned,
- Journal – what you already know about,
- Brain dump – list all of the things you know about a topic, cluster with other class members, and
- Snowball.
- Use texts or novels at more than one reading level.
- Present information through both whole-to-part and part-to-whole.
- Use a variety of reading-buddy arrangements to support and challenge students when working with different texts.
- Re-teach students pre-skills or provide enrichment for students who already demonstrate an understanding of pre-skills.
- Use texts, video or different media to convey information.
- Use Bloom’s taxonomy or Webb’s depth of knowledge to encourage thinking about content at several levels.
Differentiation Process
Why:
Differentiating process is about how students make sense of new learning. What is happening in each individual brain is based on their learning preferences, multiple intelligences, and background. Learners need time to take in, reflect on and make sense of new learning before moving on. Processes help students monitor their comprehension and determine what they do and do not understand. Learning processes also allow teachers to formatively assess student progress and provide feedback in real time.
What:
There are many different words used to describe learning processes – instructional strategies, discursive strategies, comprehension strategies… all of these are ways that learners interact with and make sense of new learning. Providing more or less structured support for learning, planning for a variety of instructional strategies based on the variety of learning styles in a classroom during a unit of study, and providing opportunities for self-reflection and self-assessment, and providing individual, pair/small group and whole group learning experiences are some key ideas for differentiation process.
How:
- Assess learning styles, multiple intelligences, learning preferences, etc. to understand individual learning profiles as well as your class profile.
- Use tiered activities that allow all students to work on the same outcome but with different levels of support.
- Provide different learning experiences based on interests – i.e. when exploring mixtures and solutions, some students might choose to learn concepts through cooking, while others may learn concepts through art.
- When planning a unit of study, ensure that concepts are interacted with using a variety of modes. For example, in mathematics, a planning form for math could be based on the idea of multiple representations of mathematical ideas:
- Use a variety of comprehension strategy tactics.
- Provide choice for students for how they are going to take notes, summarize information, make connections.
- Use reflective strategies, such as:
- Think-Pair-Share
- Journaling
- Partner talk
- Save the Last Word
- Literature Circles(which also support content and product differentiation).
- Different classroom structures, such as stations/centers, choice boards, flexible grouping all allow for different processes to be occurring simultaneously.
Differentiating Product
Why:
Differentiating product allows for student choice and allows learners to use their strengths to represent their understanding. Product choices all align to curricular outcomes, so learning is not compromised. Student voice and choice increase learner engagement. Products are the way that students represent their thinking about a curricular outcome. Differentiating the type of product being created allows you to see what they know about the curricular topic rather than the skill they needed to package that representation.
What:
Product differentiation is often cited as the most common form of differentiation and is often in the form of choices. You as the teacher may provide those choices and students pick from a variety of formats, you may have students propose their own designs or a combination of the two. How much responsibility and autonomy you provide for your students will depend on factors such as student understanding of their own strengths, age and time. When providing choice, it is important to co-construct clear criteria for success so that all products, regardless of form, are all being assessed on curricular outcomes rather than the form of a product. A rule of thumb is that the same checklist/rubric/assessment tool should be able to be used for all products on the same outcome, whether they are a paper, video, play, board game, etc.
How:
- Allow students to help design product choices.
- Co-construct assessment criteria.
- Allow for varied working arrangements – individual, pair, group
- Provide for or encourage students accessing a variety of resources.
- Ensure that all products are at the same level of Bloom’s Taxonomy or Webb’s Depth of Knowledge.
- Use a common assessment tool (checklist, rubric, etc.).
Conclusion:
When teachers plan by connecting content, process, product and learning product with student readiness, interests and learning profiles, students are more engaged and are able to understand ideas with a higher level of complexity.
Works Cited
McCarthy, J. (2015, August 28). 3 Ways to Plan for Diverse Learners. Retrieved from Edutopia: https://www.edutopia.org/blog/differentiated-instruction-ways-to-plan-john-mccarthy
New South Wales Education. (2015). Decide What to Differentiate. Retrieved from Phase 4 – Differentiating Learning: http://www.ssgt.nsw.edu.au/differentiating_learning.htm
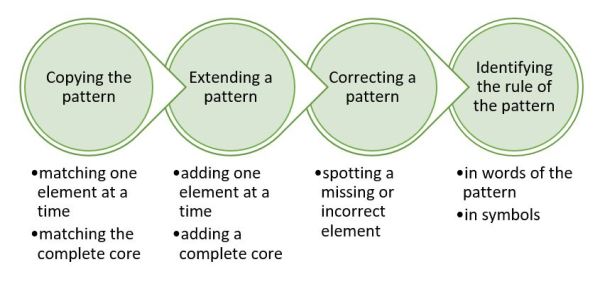
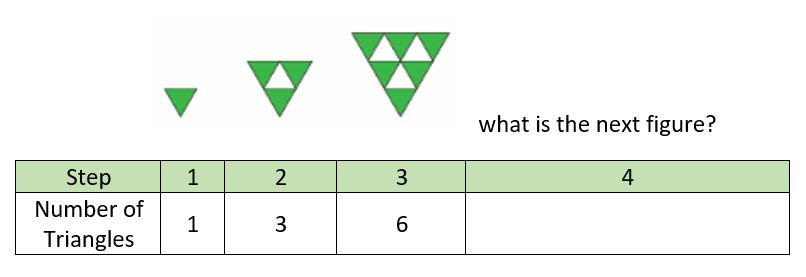
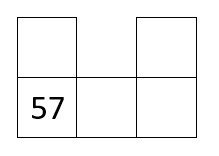
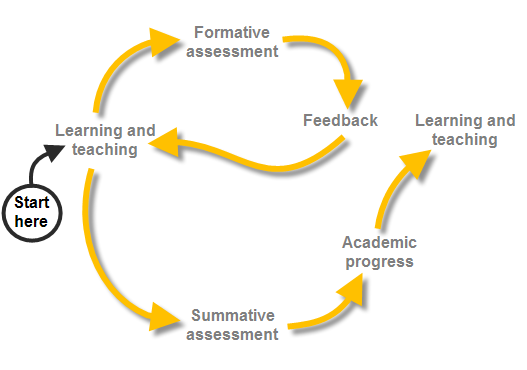
Professional development needs to surface teacher knowledge, including any misconceptions that might exist. Too often, professional learning facilitators assume that educators do not know anything so begin from the beginning… or assume that educators know everything and are choosing to resist change. I would argue teachers know a lot… and they, as a collective, want to do best for students and learning. Just like in a classroom, misconstruction of knowledge can occur. It is our job as learning facilitators to use our formative assessment skills to expose understanding and misunderstanding so that we know what to do next.
Terry Johanson Consulting 